Types of Algorithms in Machine Learning: Improve the Best Technology

Machine learning algorithms are the backbone of artificial intelligence, enabling computers to learn from data and make decisions with minimal human intervention. These algorithms are broadly categorized based on their learning style, purpose, and the type of data they process. In this comprehensive guide, we delve into the various types of machine learning algorithms, highlighting their unique characteristics, applications, and the mathematical principles that underpin them.

Supervised Learning Algorithms

An algorithm is trained on a labeled dataset in supervised learning, a kind of machine learning. The model learns to map inputs to the correct output based on the examples provided. This type of learning is analogous to a student learning from a teacher.
Click Here: Crypto with Lowest Fees

Linear Regression

To model the relationship between one or more independent variables and a dependent variable, statisticians employ the technique known as linear regression. Fitting a linear equation to the observable data is the aim.

Applications: Predicting house prices, stock market forecasting, and risk assessment.

Mathematical Principle: Minimizes the sum of the squared differences between the observed and predicted values.

Logistic Regression

Logistic regression is a tool used to solve classification difficulties, despite its name. It calculates the likelihood that an instance falls into a specific class.

Applications: Spam detection, disease diagnosis, and credit scoring.

Mathematical Principle: Uses the logistic function to squeeze the output of a linear equation between 0 and 1.

Support Vector Machines (SVM)

Support Vector Machines are powerful for both classification and regression tasks. They function by identifying the hyperplane that divides the data into classes the best.

Applications: Image recognition, text categorization, and bioinformatics.

Mathematical Principle: Maximizes the margin between different classes in the dataset.

Decision Trees

Decision trees are intuitive and easy to interpret. They split the data into subsets based on the value of input features, leading to a tree-like structure of decisions.

Applications: Loan approval, medical diagnosis, and customer segmentation.

Mathematical Principle: Recursive binary splitting of the data based on feature values.

Random Forest

An extension of decision trees, random forest combines multiple trees to improve accuracy and control overfitting.

Applications: Feature selection, predictive modeling, and recommendation systems.

Mathematical Principle: Aggregates the predictions of several decision trees to enhance robustness.

Unsupervised Learning Algorithms

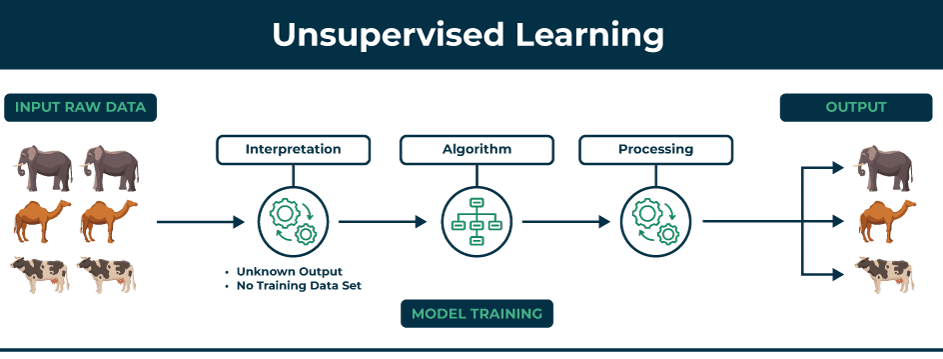
Unsupervised learning deals with unlabeled data. The algorithm tries to learn the patterns and structure from the data without any specific guidance.

K-Means Clustering

K-Means Using feature similarity as a basis, clustering divides the data into K separate clusters.

Applications: Market segmentation, image compression, and anomaly detection.

Mathematical Principle: Minimizes the sum of squared distances between points and their cluster centroids.

Hierarchical Clustering

Hierarchical clustering builds a tree of clusters. It may be divisive (top-down) or agglomerative (bottom-up).

Applications: Gene sequence analysis, social network analysis, and customer segmentation.

Mathematical Principle: Recursively merges or splits clusters based on distance metrics.

Principal Component Analysis (PCA)

Data is transformed into a set of orthogonal components using the dimensionality reduction technology known as principal component analysis.

Applications: Feature extraction, noise reduction, and data visualization.

Mathematical Principle: Identifies the directions (principal components) that maximize the variance in the data.

Independent Component Analysis (ICA)

Similar to PCA, Independent Component Analysis focuses on separating a multivariate signal into additive, independent components.

Applications: Signal processing, financial data analysis, and brain imaging.

Mathematical Principle: Maximizes the statistical independence of the estimated components.

Semi-Supervised Learning Algorithms

Semi-supervised learning falls between supervised and unsupervised learning. It uses a small amount of labeled data along with a large amount of unlabeled data for training.

Self-Training

Self-training involves a model initially trained on the labeled data, which then labels the unlabeled data to improve its performance iteratively.

Applications: Natural language processing, image recognition, and bioinformatics.

Mathematical Principle: The iterative process of augmenting the training set with its predictions.

Co-Training

Co-training uses multiple classifiers, each trained on a different view of the data. The classifiers label the unlabeled data for each other.

Applications: Web page classification, text mining, and medical diagnosis.

Mathematical Principle: Combines predictions from different perspectives to enhance learning.

Reinforcement Learning Algorithms

Reinforcement learning focuses on training agents to make sequences of decisions by rewarding them for good actions and punishing them for bad ones.

Q-Learning

Q-learning is a model-free reinforcement learning algorithm. It aims to learn the quality (Q-value) of actions, telling an agent what action to take under what circumstances.

Applications: Robotics, game playing, and automated trading.

Mathematical Principle: Uses the Bellman equation to update the Q-values iteratively.

Deep Q-Networks (DQN)

Deep Q-Networks combine Q-learning with deep neural networks, enabling the handling of high-dimensional state spaces.

Applications: Video game AI, robotics, and autonomous driving.

Mathematical Principle: Uses a neural network to approximate the Q-value function.

Policy Gradients

Policy gradient methods optimize the policy directly. They are useful for environments with continuous action spaces.

Applications: Robotics, resource management, and financial trading.

Mathematical Principle: Uses gradient ascent on the expected reward to improve the policy.

Ensemble Learning Algorithms

Ensemble learning methods combine multiple models to produce a more powerful model. The idea is to leverage the strengths of various models to improve overall performance.

Bagging

Training numerous models on various subsets of the data and averaging their predictions is known as bagging (Bootstrap Aggregating).

Applications: Reducing variance in models, improving stability and accuracy.

Mathematical Principle: Reduces overfitting by averaging multiple predictions.

Boosting

Boosting trains models sequentially, each new model correcting errors made by the previous ones.

Applications: Classification tasks, web search ranking, and risk modeling.

Mathematical Principle: Focuses on training on the mistakes of prior models to reduce bias.

By understanding and leveraging these diverse types of machine learning algorithms, we can tackle a wide array of challenges, from simple regression problems to complex image and speech recognition tasks. Each algorithm has its strengths and is best suited to specific types of data and problem scenarios.
Read more: Deep Learning Neural Networks Explained